Origin of the Golden Section-Rev 2

Last week I came across a print of some notes I made nearly 30 years ago, relating to ‘The Golden Section’ and ‘Fibonacci Numbers.’ I later transferred these on a DOS 6 computer using WordPerfect 5.1, and Autocad 9. This must have been 20 years ago.

The Golden Section.

A ratio generally recognized by humans, even if unconsciously. Considered by many people to have a major significance in biology. Like many ratios it is not a nice number to deal with, but unlike any other ratio, it has a curious family relationship.

If 0.61803398875 = ☼, then

☼ divided by 1.61803398875 = 1.000

Golden Section Ratio = 1 plus ☼

1.61803398875 / ☼ = 2.161803398875

1.61803398875 x 1.61803398875 = 2.61803398875

There are now thousands of web sites covering the Golden Section ratios and their significance in biology, so I will not go into this at present.

Fibonacci Numbers

A series of numbers created by adding together the previous two numbers, i.e.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etcetera.

If you multiply the Fibonacci numbers by the Golden Section ratio you get the following results.

1 x 1.61803398875 = 1.61803398875

2 x 1.61803398875 = 3.23667981

3 x 1.61803398875 = 4.854101964

5 x 1.61803398875 = 8.090169954

8 x 1.61803398875 = 12.94427191

13 x 1.61803398875 = 21.03444184

21 x 1.61803398875 = 33.97871375

34 x 1.61803398875 = 55.01315559

Etcetera

All very confusing, but they do appear to be very close to the Fibonacci numbers, but one term up.

However, the part number shown in Red intrigued me because I had come across this when working on the atomic structure.

(I was working in London at Shell Centre at this time, and a book I bought in the Shell bookshop was my first introduction to the Golden Section, and as I was staying in a hotel during the week I had lots of time to waste at nights).

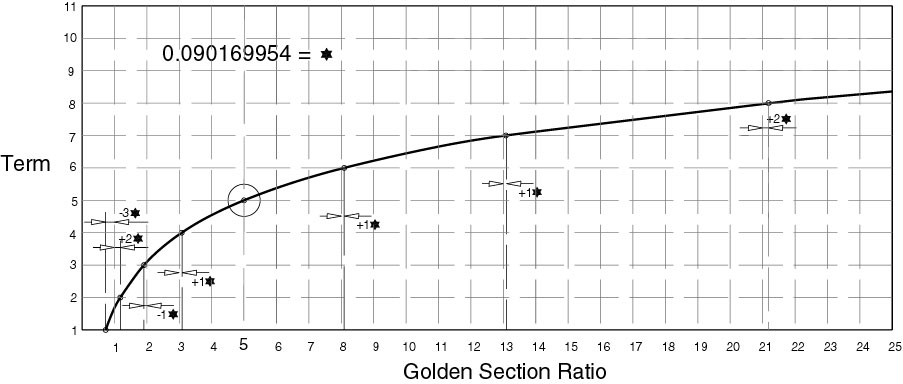
Now 1.6 + [(0.090169954/10) x 2] = 1.61803398875

Therefore I assumed that this number, 0.090169954, must be significant.

After more juggling with the figures I came up with the following result.

If 0.090169954 = ♥

Then

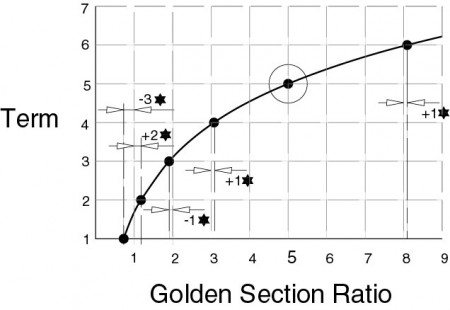
1 – (3 x ♥) = 0.7294017

1 + (2 x ♥) = 1.1803398875

2 – (1 x ♥) = 1.909830046

3 + (1 x ♥) = 3.090169954

5 + (0 x ♥) = 5.000

8 + (1 x ♥) = 8.090169954

13 – (1 x ♥) = 12.9442719

21 + (2 x ♥) = 21.1803398875

34 + (3 x ♥) = 34.27051

55 + (5 x ♥) = 55.45085006

89 + (8 x ♥) = 145.1722103

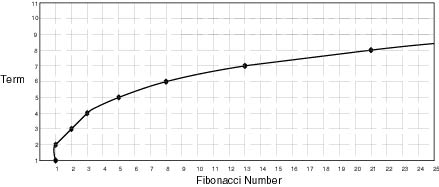
Now let us look at a graph of the Fibonacci numbers.

Not a pleasant graph to look at because there is obviously something wrong. The two points on number 1 are ridiculous.

Now let us look at the graph for the Golden Section ratio. Note this only works if you use 5 as your control point.

A closer look at the beginning of this graph may be helpful.

Now ratios can be rather difficult to explain unless they are simple ones. Millions of man-hours have been spent attempting to find a true value for Pi (π), never realizing that it is an impossible task. Each iteration changes the parameters, therefore you can never arrive at an answer. (It does have a useful purpose in that it keeps mathematicians occupied while we get on with the useful stuff.)

Logarithms are ratios and are very useful, but they are nearly always awkward numbers that you are dealing with. Pi (π) is an awkward number. The Golden Section ratio is an awkward number.

They are awkward because they relate to reality. Reality is awkward. [What an awkward word awkward is!] (From middle English ‘awk’ meaning clumsy and ‘ward’ , Anglo-Saxon, meaning direction. Logical, I suppose)

The Golden Section ratio relates to the structure of certain atoms, and this structure controls how many molecules are built up. (Even as a child, the idea of atoms with whizzing electrons seemed completely illogical, and as I grew older it became obvious that the idea was impossible)

The Golden Section ratios align with the dodecahedron.

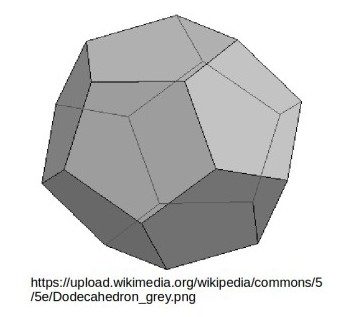
If  the octagonal faces are inscribed within a 1cm radius circle then the distance across opposite faces of the dodecahedron is 2.61803398875cm.

The Golden Section ratio is a fact of life. There are other important ratios, but none have had the same importance or interest as the Golden Section.

Nature has to handle the problems caused by the Golden Section ratio. It would be nice if nature worked with the simpler Fibonacci numbers, but this is not possible.

Nature can produce numbers such as 1,2,3,5,8,13,21 etcetera, as in arms, legs, antenna, fingers but it is not easy, and it does not always get it right. Possibly evolution depends on the problems nature has with the Golden Section ratio.

THIS IS A PRELIMINARY POSTING FOR DISCUSSION PURPOSES. IT IS APPROXIMATELY 30 YEARS OLD AND IS QUITE LIKELY TO HAVE BEEN SUCCEEDED BY LATER RESEARCH. THERE ARE SO MANY ARTICLES ON THIS SUBJECT THAT I HAVE BEEN UNABLE TO FIND THE TIME TO CHECK THEM. NOTE:

I am familiar with the standard mathematical notation with regards to Fibonacci. (I was given a personal lecture by the late Professor Laithwaite on this.) Unfortunately, like most mathematics, it does not explain anything,

Author; Brian Williams.

See also ; How to Build an atom